Needs: 9 Apples Base Game and 9 Apples Booster Pack (NOTE: The base game comes with eight cards of each number, both positive and negative)
Age Level: Grade 3
Learning Objectives: Understand the concept of multiplication: what does multiplication really mean and how we may visualize a multiplication problem. Describe why knowing how to multiply numbers is important.
What does it mean to “multiply”? As teachers, most of us have done it for many years; we may even take it for granted. But we must be able to teach our students not only the standard multiplication tables, but also an understanding of what multiplication really is, and why it is important.
So how do we define multiplication? Merriam-Webster’s Dictionary defines multiplication as follows:
Age Level: Grade 3
Learning Objectives: Understand the concept of multiplication: what does multiplication really mean and how we may visualize a multiplication problem. Describe why knowing how to multiply numbers is important.
What does it mean to “multiply”? As teachers, most of us have done it for many years; we may even take it for granted. But we must be able to teach our students not only the standard multiplication tables, but also an understanding of what multiplication really is, and why it is important.
So how do we define multiplication? Merriam-Webster’s Dictionary defines multiplication as follows:
“a mathematical operation that at its simplest is an abbreviated
process of adding an integer to itself a specified number of times
and that is extended to other numbers in accordance with laws
that are valid for integers”
process of adding an integer to itself a specified number of times
and that is extended to other numbers in accordance with laws
that are valid for integers”
To rephrase, multiplying two numbers is just shorthand for repetitive addition--for adding one number to itself over and over again, the number of times depending on what number you have multiplied it by. We can use our cards to demonstrate this idea visually, and make it more clear to our students.
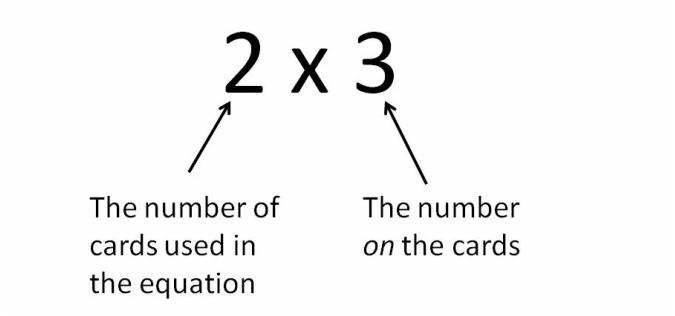
For example, let’s say we want to explore the problem 2 x 3:
For example, let’s say we want to explore the problem 2 x 3:
We may think of this as two of the number 3 being added. Using our cards to visualize this problem, we may think of the first number in the equation as the number of cards used, and the second number as the number on the cards:
This translates our multiplication problem into an addition problem: 3 + 3. Now we may use our cards again:
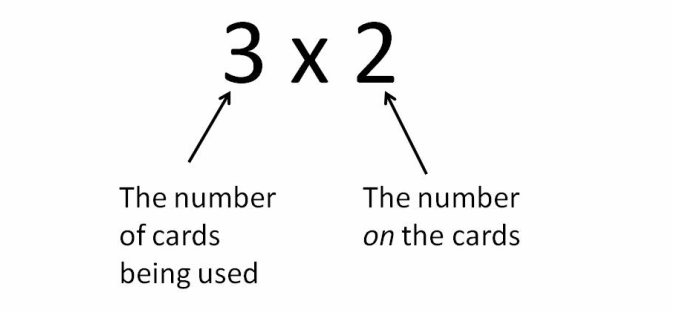
We know 3 + 3 = 6, and this is the same as 2 x 3. To satisfy ourselves that the problem will work the same way if we reverse the 3 and the 2, we may use the same visual test. The new problem:
Applying our rule as before, three is now the number of cards, and two is the number on the cards:
Translating our equation into an addition problem, we have 2 + 2 + 2:
We know 2 + 2 + 2 = 6, the same as our previous answer. We can therefore see that 3 x 2 = 2 x 3.
Let’s try another equation: 6 x 5:
As per our rule, there are six cards needed, each with the number 5. This addition problem looks like this:
If we add or count the apples, we know that 5 + 5 + 5 + 5 + 5 + 5 = 30. This is the same as 6 x 5 (or 5 x 6). We are also beginning to see something important--how much more work it is to add 5 six times! We are starting to see how much faster multiplication is, and therefore how important it is.
Let’s do one more, 8 x 9:
As per our rule, there are eight cards used, each with the number 9. This addition problem looks like this:
Adding or counting the apples, we know that 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 72, the same as 8 x 9 (or 9 x 8). It should also by now be very clear how much easier it is to remember that 8 x 9 = 72, instead of having to add 9 to itself so many times! While our cards only go up to the number 9, it should be easy to imagine how difficult trying to add very big numbers would be (11 x 15 for instance, or 250 x 373)! Using multiplication offers us a fast and easy solution!
Now that your students understand what multiplication is, and why it’s so important, help them practice their skills in multiplying numbers by playing the 9 Apples Base Game with Booster Pack! See a tutorial on how to play by clicking here.








 RSS Feed
RSS Feed
